之前的项目中用到了FTRL,在最近的交流中经常被问及这方面的相关基础,发现之前对在线学习的基础知识掌握不全面,以及对OGD和SGD等效性没有理论依据,这里作为总结。
本文参考资料losteng的csdn和雷天琪的回答
在线学习算法相关背景
在线学习算法强调的是训练的实时性,面向流式数据,每次训练不使用全量数据,而是以之前训练好的参数为基础,每次利用一个样本更新一次模型,是属于增量学习的一部分,从而快速更新模型,提高模型的时效性。
在线学习算法与离线学习关注点的不同
统计学习的先验假设是数据存在自己一定的分布,我们的目的是寻找与实际分布距离最小的策略来泛化未知的结果。数据由真实模型产生,如果能有无限数据、并在包含有真实模型的空间里求解,也许我们能算出真是模 型。但实际上我们只有有限的有噪音的数据,这又限制我们只能使用相对简单的模型。所以,理想的算法是能够用不多的数据来得到一个不错的模型。
离线学习算法强调的是数据中不断训练已有的模型,不断迭代达到真实的数据分布,在训练过程中,所有数据都是可见的,目标是一定的(就是最终的那个真实分布),其中可以采用不同的更新策略和采样策略,所以有了批量梯度下降和随机梯度下降等算法。
但是,在线学习算法的关注点是不同的,在线学习算法的限制条件是只能看到过去的数据和当前的数据,看不到未来的数据,所以我们训练的策略可能是任意的数据分布,通过不断的训练可能颠覆之前的训练结果,所以在线学习甚至是为了破坏我们之前的策略精心设计的。
在线学习关注点在于,追求对所知道的所有知识所能设计最优的策略,那么同这个最优的策略的差距成为后悔(regret):后悔没有从一开始就选择这个策略,当然,我们希望的是,随着时间的增加,这个差异会不断的变小。因为我们不对数据进行任何假设,所以策略是否完美并不是我们关心的(比如回答所有问题),我们追求的是,没有后悔(no-regret)
batch模式和delta模式
梯度下降可以分成两种模式,batch模式和delta模式。batch模式的时效性比delta模式要低一些。分析一下batch模式,比如昨天及昨天的数据训练成了模型M,那么今天的每一条训练数据在训练过程中都会更新一次模型M,从而生成今天的模型M1。
batch学习可以认为是离线学习算法,强调的是每次训练都需要使用全量的样本,因而可能会面临数据量过大的问题。一般进行多轮迭代来向最优解靠近。online learning没有多轮的概念,如果数据量不够或训练数据不够充分,通过copy多份同样的训练数据来模拟batch learning的多轮训练也是有效的方法。
delta模式可以认为是在线学习算法,没有多轮的概念,如果数据量不够或训练数据不够充分,通过copy多份同样的训练数据来模拟batch learning的多轮训练也是有效的方法。所以,OGD和SGD都属于在线学习算法,因为每次更新模型只用一个样本。SGD则每次只针对一个观测到的样本进行更新。通常情况下,SGD能够比GD“更快”地令 逼近最优值。当样本数 特别大的时候,SGD的优势更加明显,并且由于SGD针对观测到的“一条”样本更新 ,很适合进行增量计算,实现梯度下降的Online模式(OGD, OnlineGradient Descent)。
在线凸优化
本章只是简单介绍,如果想要深入了解在线凸优化(OCO),强烈推荐阅读Elad Hazand的著作和Zinkevich的Paper
聊到在线学习算法通常会说到专家系统,在$t$时刻专家$i$的损失是$\ell_t(e^i)$,于是这个时刻Weighted Majority(WM)损失的期望是$\sum_{i=1}^m w_t^i\ell_t(e^i)$,是关于这m个专家的损失的一个线性组合(因为权重$w_t^i$关于$i$的和为1,所以实际上是在一个simplex上)。将专家在$t$时刻的损失看成是这个时候进来的数据点,于是我们便在这里使用了一个线性的损失函数。
WM的理论证明可以参考Littlestone 94,Freund 99,虽然在上个世纪已经完成,但是将其理论拓展到一般的凸的函数还是在03年由Zinkevich完成的。
在线梯度下降(OGD)
Zinkevich提出的算法很简单,在时刻t做两步操作,首先利用当前得到数据对$h_t$进行一次梯度下降得到$h_{t+1}$,如果新的$h_{t+1}$不在$\mathcal{H}$中,那么将其投影进来:
$$\displaystyle h_{t+1}=\Pi_{\mathcal{H}}(h_t-\eta_t\nabla\ell_t(h_t))$$
这里$\nabla\ell_t(h_t)$是$\ell_t(h_t)$关于$h_t$的导数(如果导数不唯一,就用次导数),$\eta_t$是学习率,$\Pi_{\mathcal{H}}(\cdot)$是投影子,其将不在$\mathcal{H}$中的向量$x$投影成一个与$x$最近的但在$\mathcal{H}$中的向量(如果$x$已经在$\mathcal{H}$中了,那就不做任何事),用公式表达就是$\Pi_{\mathcal{H}}(x)=\arg\min_{y\in\mathcal{H}}|x-y|$。此算法通常被称之为 Online Gradient Descent。
先来啰嗦几句其与离线梯度下降的区别。在离线的情况下,我们知道所有数据,所以能计算得到整个目标函数的梯度,从而朝最优解 迈出坚实的一步。而在online设定下,我们只根据当前的数据来计算一个梯度,其很可能与真实目标函数的梯度有一定的偏差。我们能保证的只是会减小的值,而对别的项的减少程度是未知的。当然,我们还是一直在朝目标前进,只是可能要走点弯路。
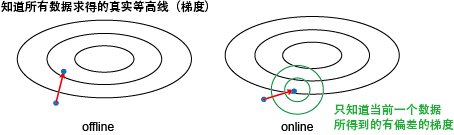
那online的优势在哪里呢?其关键是每走一步只需要看一下当前的一个数据,所以代价很小。而offline的算法每走一个要看下所有数据来算一 个真实梯度,所以代价很大。假定有100个数据,offline走10步就到最优,而online要100步才能到。但这样offline需要看1000 个数据,而online只要看100个数据,所以还是online代价小。
在这里,$\mathcal{H}$的作用是什么呢?记得在ML中的目标函数通常是损失+罚$\ell(h)+\lambda f(h)$的形式。例如ridge regression就是平方误差+$\ell_2$罚,lasso是平方误差+$\ell_1$罚,SVM是hinge loss+$\ell_2$罚。最小化这个目标函数可以等价于在$f(h)\le\delta$的限制下最小化$\ell(h)$。$\lambda$和$\delta$是一一对应的关系。实际上$f(h)\le\delta$就是定义了一个凸子空间,例如使用$\ell_2$罚时就是一个半径为$\delta$的球。所以,Online Gradient Descent可以online的解这一类目标函数,只是对于不同的罚选择不同的投影子。
下面是理论分析。记投影前的 $\tilde h_{t+1} = h_t-\eta_t\nabla\ell_t(h_t)$,以及offline最优解$h^=\arg\min_{h\in\mathcal{H}}\sum_{t=1}^T\ell_t(h)$ 。因为$ \mathcal{H} $是凸的且 $ h^ $ 在其中,所以对 $ \tilde h_{t+1} $ 投影只会减少其与 $ h^ $ 的距离,既 $ |h_{t+1}-h^|\le|\tilde h_{t+1}-h^*| $ 。记 $ \nabla_t=\nabla \ell_t(h_t) $ ,注意到
$$\displaystyle |\tilde h_{t+1}-h^|^2=|h_t-h^|^2+\eta_t^2|\nabla_t|^2-2\eta_t\langle\nabla_t,h_t-h^*\rangle.$$
由于$\ell_t$是凸的,所以有
$$\displaystyle \ell_t(h_t)-\ell_t(h^)\le \langle\nabla_t,h_t-h^\rangle \le \frac{1}{2\eta_t}\big(|h_t-h^|^2 - |h_{t+1}-h^|^2\big) + \frac{\eta_t}{2}|\nabla_t|^2.$$
取固定的$\eta_t=\eta$,对$t$进行累加就有$R(T)\le \frac{1}{2\eta}|w_1-w^*|^2+\frac{\eta}{2}\sum_{t=1}^T|\nabla_t|^2$。记$\mathcal{H}$的直径为$D$,且对所有$t$有$|\nabla_t|\le L$成立(既Lipschitz常数为$L$),再取$\eta=\frac{D}{L\sqrt{T}}$,那么
$$\displaystyle R(T)\le LD\sqrt{T}.$$
这个bound可以通过设置变动的学习率$\eta_t$加强。
FTRL更新公式和SGD更新公式的等效性
SGD算法的迭代计算公式如下:
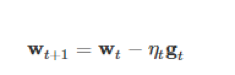
其中 t 为迭代轮数,w是模型参数,g是loss function关于w的梯度,而η是学习率。
FTRL算法的迭代算公式如下:
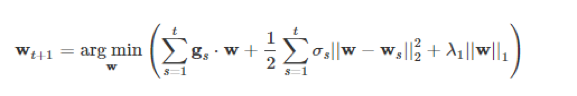
其中 t 为迭代轮数,w是模型参数,σs定义成
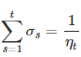
λ1是L1正则化系数。在公式2中,arg min算子的内容中由3项组成,如果我们去掉最后面的L1正则化项,公式2就变成下面的公式3:
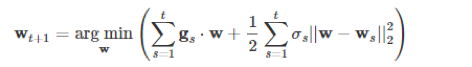
(3)式子在换个形式后就等价于梯度下降公式。
以下是推导过程:
首先,我们要求公式3中的最小值,我们可以对其求导,得到
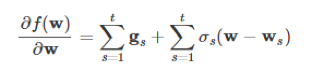
令上面的求导公式等于0就得到极值,极值正是Wt+1:
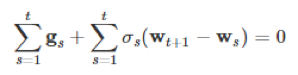
将含有wt+1的项放到等号左边,剩下的放在右边,得到公式6:
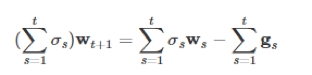
进一步化简得到公式7:

用 t-1 替换 t,得到公式8:
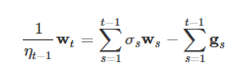
用公式7减去公式8,即式子的左边右边同时减去,得到公式9:
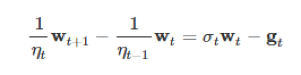
把σt用ηt表示,得到公式10:
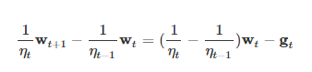
对公式10化简即可得到公式1:
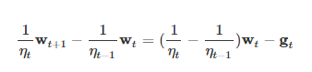
通过上面的推导证明,我们看到公式3与公式1确实等价。
