为什么要用线段树
有这样一个场景,给定一个数组,让求任意区间的累加和。
一般有两种算法
- 将这个区间上的所有数累加,然后返回
- 先求前n项的前缀和,然后将这期间差相减
但是,如果对其中任意一个数据进行操作,就会对累加和的时间复杂度有影响,第一种只需要修改一个元素,第二种却需要将其后的所有前缀和都进行修改。所以第一种查询费时间修改不费时间,第二种查询不费时间修改费时间。线段树就是为了适应修改和统计操作而设计的。
线段树的原理
线段树的原理,就是,将[1,n]分解成若干特定的子区间(数量不超过4*n),然后,将每个区间[L,R]都分解为
少量特定的子区间,通过对这些少量子区间的修改或者统计,来实现快速对[L,R]的修改或者统计。
具体可以参考线段树详解
线段树例子
由此看出,用线段树统计的东西,必须符合区间加法,否则,不可能通过分成的子区间来得到[L,R]的统计结果。
符合区间加法的例子:
- 数字之和——总数字之和 = 左区间数字之和 + 右区间数字之和
- 最大公因数(GCD)——总GCD = gcd( 左区间GCD , 右区间GCD );
- 最大值——总最大值=max(左区间最大值,右区间最大值)
不符合区间加法的例子:
- 众数——只知道左右区间的众数,没法求总区间的众数
- 01序列的最长连续零——只知道左右区间的最长连续零,没法知道总的最长连续零
线段树的递归模版(区间和模版)
定义
1 | // 注意!线段树开始是从1开始的,不是0,否则会导致root<<1不是左节点 |
建树
1 | void PushUp(int root, vector<int>& sum) { |
点修改
nums[index] += c1
2
3
4
5
6
7
8
9
10void Update(int index, int c, int l, int r, int root, vector<int>& sum) {
if (l == r) {
sum[root] += c;
return;
}
int mid = l + (r - l) / 2;
if (index < mid) Update(index, c, l, mid - 1, sum);
else Update(index, c, mid, r, sum);
PushUp(root, sum);
}
区间修改
nums[left, right] += c1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26// 下推时必须将统计值更新,子树更新时必须将父节点也上推更新,保证数据一致性
void PushDown(int root, int l_cnt, int r_cnt, vector<int>& sum, vector,int>& add) {
// 下推标记
add[root << 1] += add[root];
add[root << 1 | 1] += add[root];
// 下推统计值
sum[root << 1] += add[root] * l_cnt;
sum[root << 1 | 1] += add[root] * r_cnt;
// 清除标记
add[root] = 0;
}
void Update(int left, int right, int c, int l, int r, int root, vector<int>& sum, vector<int>& add) {
if (left <= l && r <= right) {
sum[root] += c * (r - l + 1); // 更新统计信息
add[root] += c; // 更新惰性标记
return;
}
int m = l + (r - l) / 2;
PushDown(root, m - l + 1, r - m, sum, add); // 在更新新标记的时候将旧标记下推, 分别表示左右子树的更新个数
if (left <= m) Update(left, right, c, l, m, root << 1, sum, add);
if (m < right) Update(left, right, c, m + 1, r, root << 1 | 1, sum, add);
PushUp(root, sum); // 因为只下推了就标记,所以需要更新本节点的统计值
}
查询区间
1 | int Query(int left, int right, int l, int r, int root, vector<int>& sum, vector<int>& add) { |
非递归原理和实现
后期更新…
线段树思路
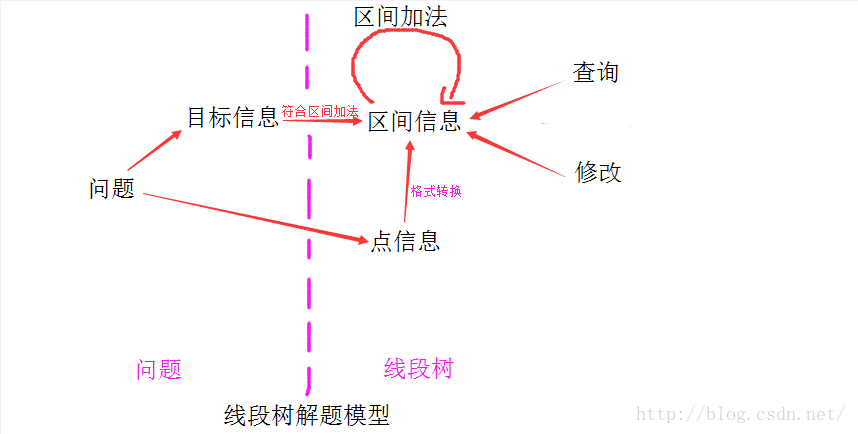
题目练习
区间最大值(头条面试题)
1 |
|
区间和
1 | // 2019-04-13 |
最大公因数
因为最大公因数对于加减没有惰性标记代表性,所以这里采用乘除作为update的参数
update(L,R, c, l, r, root)代表给L到R的所有数都乘以c
1 | // 2019-04-13 |
字符串哈希
待补充。。。
最长连续零
待补充。。。
计数排序
待补充。。。
扫描线
待补充。。。
